The Cyclic Redundancy Check (CRC) for AX.25
This article describes basic implementation and testing of the cyclic redundancy check (CRC) for the AX.25 amateur packet radio protocol (also defined by CRC-CCITT and in ISO 3309).
1 Overview of the AX.25 CRC
The AX.25 CRC is used by amateur radio terminal node controllers (TNC) to produce a frame-check sequence (FCS) for error detection. A basic implementation of the CRC for AX.25 uses a shift register and XOR operations. While not optimized for processing speed, the implementation provided here is practical and illustrative.
The AX.25 CRC is described by the characteristics given in the following table.
| Names associated with the AX.25 CRC protocol | CRC-CCITT, CRC-16-X25, CRC-16-CCITT |
| Degree of polynomial | 16 |
| Generator polynomial | G(x) = x16+x12+x5+1 |
| Polynomial in hex notation | 0x1021 |
| Bit order | Reflected input byte (LSB of byte sent first) |
| Initial value | 0xFF |
| Output XOR mask | 0xFF (bitwise-invert shift register to produce frame check sequence) |
2 Implementation of the AX.25 CRC with a Shift Register
Figure 1 shows a shift-register implementation of the CRC algorithm for AX.25. This CRC generator uses the CRC-CCITT generator polynomial 0x1021. The 16-bit shift register is initialized with all ones (0xFFFF). The each numbered block is a stage of the shift register and holds one bit. The “+” circles indicate the XOR operation. The shift register bit values shift to the right. XOR operations are applied between shift register stages as indicated in the figure; for example, during a shift, the value of stage 5 is XORed with the feedback value, and the XOR result is stored in stage 6. The value shifted into stage 1 is a zero XORed with the feedback value; this is equivalent to shifting the feedback value into stage 1, but XORing with a zero is illustrative of the method used in software where a bitwise-XOR mask is applied to the shift register after the shift is performed.
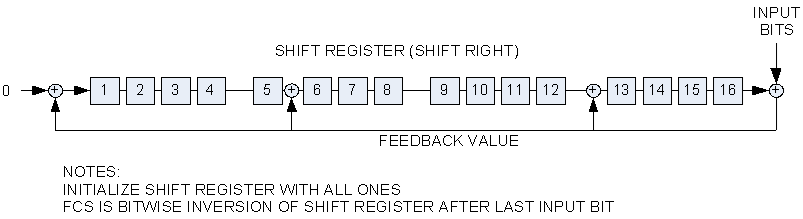
Figure 1. Shift-register implementation of the CRC-CCITT for AX.25.
3 Implementation of the AX.25 CRC in MATLAB
The m-file at the following link includes a function that implements the AX.25 CRC algorithm in MATLAB. This function implements the AX.25 algorithm as shown in Figure 1.
4 Testing the AX.25 CRC MATLAB Algorithm
The MATLAB CRC algorithm was tested against known input and output values for the CRC calculation. Three test cases are given here:
- Input and output values using an actual AX.25 frame
- Input, output, and intermediate values using a 24-bit sequence
- Input and output values using a common test sequence
4.1 Test Values Using an AX.25 Frame
An unnumbered information frame was sent using a PacComm PicoPacket TNC. The output waveform (audio FSK) of the TNC was captured, demodulated, and decoded on a PC using MATLAB. The decoded fields are as follows:

This frame was produced using the TNC by putting the TNC into “converse” mode, pressing the character “A”, and pressing enter. The FCS is calculated by applying the CRC algorithm to the bits between the AX.25 start flag (01111110) and the FCS field that is appended to the end of the frame before the end flag (see [1] for AX.25 frame construction). The demodulated bits from the TNC used for the FCS calculation were:
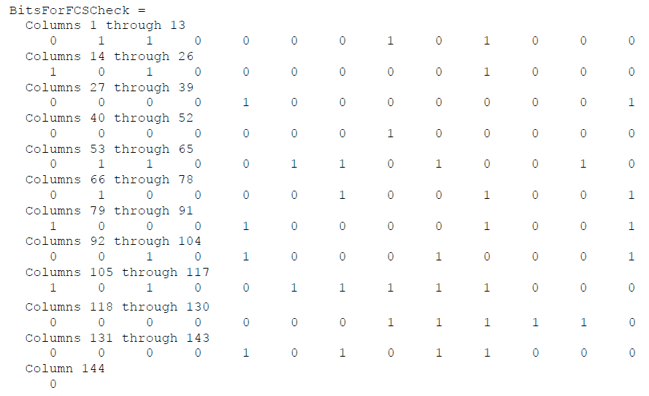
The FCS appended to the end of the frame by the TNC were:
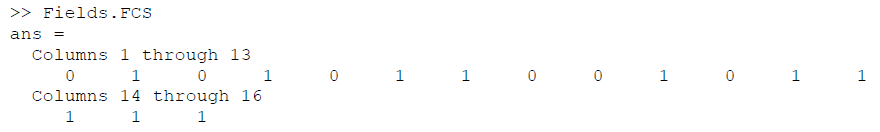
The frame bits were used as input to the MATLAB CRC algorithm. The FCS calculated by the MATLAB CRC algorithm was:

The FCS appended by the TNC and the FCS produced by the MATLAB algorithm match. Both operated independently on the same input frame bits.
4.2 Simple Test Values with Intermediate Values
The input bits for this test represented the ASCII values of “ABC” with the least-significant bit (LSB) first in the order sent.

The 24 input bits used for the test were:

(First bit sent is on left.)
The intermediate states of the shift register are (stage 1 of shift register is in left column):
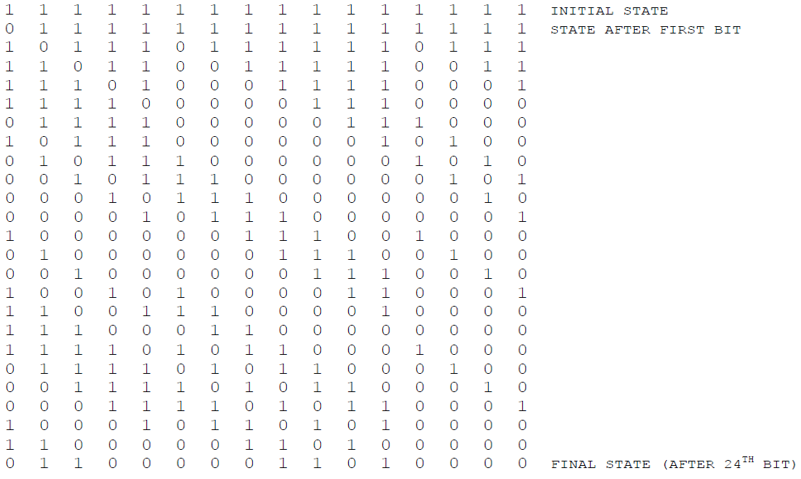
The FCS is the bitwise inversion of the final state. The FCS is:

The MSB of the FCS is on the left; the MSB is sent first for AX.25 protocol (see [1]).
4.3 A Common Test Value and Bit-order Reversal
A commonly used test sequence contains the ASCII values representing the string “123456789” with the least-significant bit (LSB) of the first character sent first. The test bit sequence is (first bit in upper left with bits read left to right in each row):

Using the above bits as an input, the output of the MATLAB CRC algorithm is:
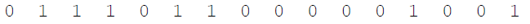
Some references report the CRC-CCITT result of “123456789” to be the hex value 0x906E (see [2]). This hex value corresponds to the binary value:

This is equivalent to the result of the MATLAB CRC algorithm with the bit order reversed. When reversed in bit order, 0x906E corresponds to:

The MATLAB CRC algorithm produces the first bit sent on the left, just like the amateur radio TNC. The output reported by [2] contains the first bit sent on the right compared to the output of the amateur radio TNC.
5 References and Links
[1] AX.25 Amateur Packet-Radio Link-Layer Protocol, Version 2.0, October 1984. See http://www.tapr.org/pub_ax25.html
[2] From http://users.physik.tu-muenchen.de/gammel/matpack/html/LibDoc/Crypto/MpCRC.html (no longer a valid link)
This information is based on an amateur packet radio project by Bill Newhall and Ileana Carrasquillo in 2008.
Source file: CRC_for_AX25_Rev_2008-11-23.doc
Revision: 11/23/2008



